|
|
|
Mini-coursesClassical topics Chikako Mese - Twisted Harmonic mappings This set of lectures will cover the following topics:
Julien Marché - Character Varieties for Finitely Presented Groups These three lectures give an overview of character varieties of finitely generated groups. The plan of the course is to provide examples, applications and some proofs of the following topics.
Adam Jacob - From Higgs bundles to local systems In this mini course we will present the work of Simpson, and demonstrate how to construct flat connections on stable Higgs bundles over compact complex manifolds. Our approach to this construction will be to follow the gradient flow of a functional on the space of Hermitian structures on our bundle. We will present the analytic difficulties one must overcome in order to show that this flow converges, and furthermore relate this construction to various other notations of stability in complex algebraic geometry. Catriona Mac Lean and Philippe Eyssidieux - Hodge Theory and Griffiths’ theory We will start by defining the basic objects of Hodge theory, namely real and complex polarized Hodge structures and polarized variations of Hodge structures, followed by a discussion of the differential geometric properties of Griffiths' period mapping of a polarized variation of Hodge structure. We will concentrate especially on the homogenous structure of the period domain and its dual, as well as the horizontal tangent space and the curvature properties of the homogenous vector bundles, particularly the Hodge bundles, the determinant line bundle, and the horizontal tangent space. In the last lecture, we will present mixed Hodge structures and the SL2 orbit theorem essentially reducing it to the existence of the limiting Mixed Hodge Structure of a quasi unipotent Variation of Hodge Structures on the punctured disk. Bertrand Rémy - Buildings This course will be dealing with affine buildings. The latter spaces are products of simplicial complexes and play a role analogous to that of Riemannian symmetric spaces when the relevant algebraic group is defined over a non-archimedean local field and no longer over the real or the complex numbers. Many well-known properties in the archimedean context are still valid for affine buildings, the most important one being non-positive curvature. We will discuss the construction of affine buildings and explain why reductive groups over valued fields act on suitable buildings in a very balanced way.
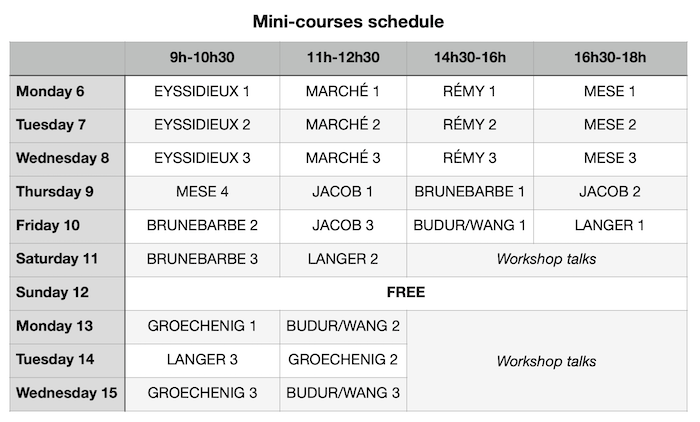
Advanced topics Yohan Brunebarbe - o-minimality and period mappings A source of major complications in the study of variations of Hodge structures comes from the fact that the parameter spaces for Hodge structures (i.e. the arithmetic quotients of period domains), which are complex analytic spaces by construction, are only rarely algebraic. It has been recently proved by Bakker-Klingler-Tsimerman that the classical constructions in variational Hodge theory were naturally taking place in an intermediate category, namely the analytic spaces that are definable in a o-minimal structure. The objects in this category enjoy important finiteness properties, providing a framework for doing tame complex analytic geometry, and this point of view has already been fruitful in applications. My lectures will be an introduction to this circle of ideas, starting with an introduction to o-minimal geometry with a view towards algebraization theorems. Nero Budur and Botong Wang - Absolute sets of local systems We show that natural (derived) functors on constructible sheaves on smooth complex algebraic varieties can be used to construct a special kind of constructible sets of local systems, called absolute sets. We characterize the absolute sets in the rank one case as boolean combinations of torsion-translated complex algebraic tori. Michael Gröchenig - Simpson’s integrality Conjecture This mini-course is devoted to the theory of rigid local systems on complex varieties with a particular focus on Simpson’s integrality conjecture. We will discuss joint work with Hélène Esnault concerning integrality for cohomologically rigid local systems. Adrian Langer - Moduli spaces for flat connections and Higgs bundles The aim of this mini-course is to describe construction and basic properties of moduli spaces of semistable Our approach will be algebraic allowing for constructions of moduli schemes in arbitrary (also mixed) characteristic. Schedule
|