|
|
|
WorkshopList of speakers : The last part of the summer school (mainly the second week) will be devoted to a workshop on Non abelian Hodge Theory and its applications to Algebraic Geometry. The speakers in the list below will give research talks on some recent advances in the field.
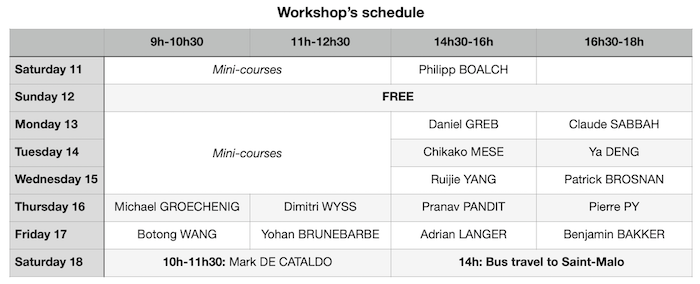
Schedule of the workshop
Titles and abstracts
Ben Bakker -- Period integrals of algebraic varieties Period integrals on complex algebraic varieties are the integrals of algebraic differential forms along topological cycles. They are at the heart of Hodge theory. In this talk I will survey some recent results on the behavior of the functions obtained by taking period integrals in algebraic families, including an Ax--Schanuel type theorem on their transcendence, some geometric applications, and the relationship to the Grothendieck period conjecture. This is joint work with J. Tsimerman. Philipp Boalch -- Diagrams, nonabelian Hodge moduli spaces and global Lie theory The classical theory of systems of linear differential equations in the complex domain morphed into the theory of connections on curves, and then morphed again into “2d gauge theory”, a highpoint being the nonabelian Hodge theorem of Hitchin–Simpson–Corlette–Donaldson. However along the way, a sleight of hand was done: the passage to compact Riemann surfaces, thereby avoiding the tricky problem of understanding boundary conditions on noncompact Riemann surfaces. The good news is that these tricky problems were solved by mathematicians working in France some 20 years ago, a key step being to understand the classical papers on irregular singularities. This led to the wild nonabelian Hodge theorem on curves, and a huge bestiary of new complete hyperkahler manifolds, now encompassing the classical examples of integrable systems stemming from work of Painleve, Schlesinger, Garnier, Moser, Mumford, Seiberg-Witten and others. Due to Simpson's construction problem it is possible that all examples occur in the case of curves. In this talk I’ll review some of the simplest examples, sketch how to describe them topologically in terms of Stokes local systems (generalising the usual fundamental group representations) and explain recent steps to define a theory of “Dynkin diagrams” to classify these new nonabelian Hodge moduli spaces. Parallel to the theory of representations of Lie groups it is convenient to make an abstract definition of a “nonabelian Hodge space”, and then study different “representations” of such spaces, involving different rank bundles and pole configurations/orders, accounting for different Lax pairs of many integrable systems or isomonodromy systems. Patrick Brosnan -- Extensions in MHM and Hain's biextension line bundle (joint with Greg Pearlstein) The so-called biextension line bundle L is an analytic line bundle over a complex manifold U associated to a pair of normal functions on U. In the case that U is a complement of a normal crossing divisor in a projective variety S and the two normal functions are admissible, Pearlstein and I proved that (a) L can be extended to a line bundle on S and (b) L has a canonical extension to S as a Q-line bundle. (a) proves that L has an algebraic structure, but (b) begs the question of describing what the extension is. The first Chern class of L in the cohomology of U is a topological invariant of the normal functions which is classical to compute. (I.e., it goes back to the foundational papers of Hain and Hain-Reed.) In this talk, I will give a formula for the Q-line bundle as a Yoneda product in Saito's category of mixed Hodge modules. Yohan Brunebarbe -- Hyperbolicity in presence of a large local system Serge Lang has proposed several influential conjectures relating different notions of hyperbolicity for proper complex varieties. I will prove that some of these conjectures are true for varieties admitting a large complex local system. Mark Andrea de Cataldo -- Cohomology of Higgs moduli via positive characteristic I will review the P=W Conjecture relating the singular cohomology of the moduli space of Higgs bundles on a curve with the one of the corresponding character variety. I will then explain how certain symmetries of this cohomology, which are predictions of the P=W Conjecture, can be constructed using techniques from non-abelian Hodge theory in positive characteristic. Based on joint work with Davesh Maulik, Junliang Shen, and Siqing Zhang. Ya Deng -- Representation of fundamental groups and logarithmic symmetric differential forms Complex projective manifolds with infinite fundamental groups are conjectured to admit global symmetric differential forms. In 2013, Brunebarbe, Klingler and Totaro proved that any compact Kähler manifold has symmetric differential forms if there is a linear representation of its fundamental group with infinite image. In this talk I will explain a joint work with Brotbek, Daskalopoulos and Mese on the extension of BKT's theorem to quasi-projective cases. Daniel Greb -- Cycles in the K3 period domain and moduli of complex hyperkähler metrics Hyperkähler metrics on K3 surfaces give rise to rational curves of degree 2 in the K3 period domain, socalled "twistor lines". While these are used in the proofs of many deep results, their existence also implies that the group of isometries of the K3 lattice does not act properly discontinuously on the period domain, preventing a moduli space of unpolarised complex K3 surfaces to exist. I will report on work in progress with Martin Schwald (Essen), in which we study the cycle space of the K3 period domain. This space parametrises twistor lines as part of its real locus, but also all their degenerations and complex deformations as submanifolds of the period domain. I will explain how many foundational problems regarding the moduli theory of K3s disappear when passing to the cycle space and also indicate how the original version of Penrose's Twistor Theory (the "nonlinear graviton" construction) can be used to understand what kind of geometric structure a small complex deformation of an honest twistor line corresponds to. Michael Groechenig -- Complex K-theory of dual Hitchin systems Let G and G’ be Langlands dual reductive groups (e.g. SL(n) and PGL(n)). According to a theorem by Donagi-Pantev, the generic fibres of the moduli spaces of G-Higgs bundles and G’-Higgs bundles are dual abelian varieties and are therefore derived equivalent. It is an interesting open problem to prove existence of a derived equivalence over the full Hitchin base. I will report on joint work in progress with Shiyu Shen, in which we construct a K-theoretic shadow thereof: natural equivalences between complex K-theory spectra for certain moduli spaces of Higgs bundles (in type A). Adrian Langer -- Some applications of non-abelian Hodge theory in positive characteristic I will talk about recent applications of Ogus-Vologodsky correspondence to study some classical problems in algebraic geometry. In particular, I will talk about strong semipositivity theorems for analogs of complex polarized variations of Hodge structures and their generalizations. Chikako Mese -- Infinite energy harmonic maps and rigidity In this talk, we discuss the generalization of Mochizuki’s result on non-Abelian Hodge theory of quasi-projective varieties in the Archimedean case to arbitrary Lie groups and prove a non-Archimedean version of the same result. This approach involves infinite energy harmonic maps from quasi-projective varieties to symmetric spaces and Euclidean buildings. Pranav Pandit -- Fukaya categories and the Hitchin system I will review the conjectural picture relating the base of the Hitchin system to Bridgeland stability conditions on Fukaya categories, and discuss some recent progress. Pierre Py -- Subgroups of hyperbolic groups, finiteness properties and complex hyperbolic lattices Following C.T.C. Wall, we say that a group G is of type F_n if it admits a classifying space which is a CW-complex with finite n-skeleton. For n=2 one recovers the notion of being finitely presented. We prove that in a cocompact arithmetic lattice in the group PU(m,1) with positive first Betti number, deep enough finite index subgroups admit plenty of homomorphisms to Z with kernel of type F_{m-1} but not of type F_m. This provides many non-hyperbolic finitely presented subgroups of hyperbolic groups and answers an old question of Brady. This is based on a joint work with C. Llosa Isenrich. Claude Sabbah -- Airy and Hodge Symmetric powers of the classical Airy differential equation are complex analogues of symmetric power moments of cubic exponential sums. Although these equations have irregular singularities, their de Rham cohomology underlies an arithmetic Hodge structure in the sense of Anderson. Their Hodge numbers are computed by means of the irregular Hodge filtration, which is indexed by rational numbers, on their realizations as exponential mixed Hodge structures. All these Hodge numbers are either zero or one. This is a joint work with Jeng-Daw Yu. Botong Wang -- Perverse sheaves on varieties with large fundamental group and the Singer-Hopf conjecture The Singer-Hopf conjecture predicts that for a compact aspherical manifold $X$ of real dimension $2n$, the Euler characteristic of $X$ has sign $(-1)^n$. In a joint work with Youngqiang Liu and Laurentiu Maxim, we made a stronger conjecture in the complex algebraic geometric setting that if a smooth complex projective variety is aspherical, then all perverse sheaves on the variety has non-negative Euler characteristics. In a joint work with Donu Arapura, we confirm this conjecture in a special case, when the fundamental group admits a faithful, semisimple, cohomologically rigid representation. Our approach is to construct a complex VHS on the variety to relate the nonnegativity of Euler characteristics with certain curvature conditions on the period domain. Dimitri Wyss -- BPS-invariants for Higgs bundles from non-archimedean integrals BPS-invariant appear, when one tries to count sheaves on a Calabi-Yau 3-fold in the presence of strictly semi-stable objects as a sort of reduced theory. In joint work with Francesca Carocci and Giulio Orecchia we consider the special case when the CY3 fold is a local curve (or surface) giving rise to moduli spaces of Higgs bundles. We conjecturally give a new definition of (refined) BPS-invariants in this case using non-archimedean integration. To support our conjecture, we prove an invariance property of our integrals, which has recently been established for classical BPS-invariants by Maulik-Shen and Kinjo-Koseki. Ruijie Yang -- Decomposition theorem for semisimple local systems In complex algebraic geometry, the decomposition theorem asserts that semisimple geometric objects remain semisimple after taking direct images under proper algebraic maps. This was conjectured by Kashiwara and was proved by Sabbah and Mochizuki in a series of seminal papers via non-abelian Hodge theory on quasi-projective varieties and D-module theoretic techniques. In this talk, I will explain a new proof in the case of semisimple local systems, using a new Weil operator on the cohomology of semisimple local systems via twistor theory and a topological approach adapting de Cataldo-Migliorini. Joint work with Chuanhao Wei. |